Математика 3 клас. Урок 110
Мета: познайомити учнів із розв'язуванням рівнянь, у яких один із компонентів поданий виразом зі змінною; закріплювати вміння розв'язувати задачі вивчених видів; розвивати вміння думати, спостерігати, класифікувати, узагальнювати; виховувати інтерес до математики.

Хід уроку
I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
1. Перевірка домашнього завдання
Завдання 983
360: 10 = 36
360:30 = 36:3 = 12
630 : 7 = 90
630: 14 = 90:2 = 45
280 : 4 = 70
280: 20 = 70: 5 = 14
540 : 9 = 60
540: 18 = 60:2 = 30
Завдання 984
— Скільки намистин у кожному зразку? ((60 + 60 : 2): 3 = 30 (нам.))
2. Математичний диктант
— Запишіть вирази, знайдіть їх значення.
• Добуток чисел 7 і 1 збільшити на добуток чисел 1 і 0.
• Суму чисел 18 і 43 помножити на 1.
• Частку чисел 0 і 8 збільшити в 7 разів.
• Перший множник 1, другий — на 49 більше. Знайти добуток.
• Різницю чисел 20 і 19 помножити на їх суму.
• Частку чисел 10 і 10 збільшити на добуток цих чисел. Відповіді:
71 + 10=7 1•(1 + 49) = 50
(18 + 43) • 1 = 61 (20 - 19) • (20 + 19) = 39
0:8-7 = 0 10: 10+10•10 = 101
3. Розв'язування прикладів з коментуванням (18+ 27): 3 (16+ 36): 4
— Які числа ділили? На які доданки розкладали?
Далі вчитель за допомогою учнів пояснює приклади на ділення трицифро-вого числа на одноцифрове шляхом розкладання діленого на зручні доданки.
112 : 7 = (70 + 42): 7 = 10 + 6 = 16
120 : 8 = (80 + 40): 8 = 10 + 5 = 15
126 : 9 = (90 + 36): 9 = 10 + 4 = 14
114 : 6 = (60 + 54) : 6 = 10 + 9 = 19
III. ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ
— Сьогодні на уроці ми ознайомимося із розв'язуванням рівнянь, у яких один із компонентів поданий виразом зі змінною.
IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Підготовча робота [с. 149, завдання 986)
— Прочитайте вирази за останньою дією.
354 - (240 - 36) (зменшуване 354, від'ємник виражений різницею чисел 240 і 36);
350 : (63 : 9) (ділене 350, дільник виражений часткою чисел 63 і 9)\ 250 : 10 • 5 (частку чисел 250 і 10 помножити на 5).
2. Розв'язування рівнянь за зразком (с. 149, завдання 986)
х: (32 -24) = 16
— Яка остання дія в поданому рівнянні? (Ділення)
— Назвіть компоненти ділення. (Ділене, дільник, частка)
— Назвіть ділене, дільник, частку.
— Яку дію можна виконати? (32 — 24 — 8) Учитель записує:
х : 8 = 16
— Який компонент нам невідомий? (Ділене х)
— Як знайти ділене? (Потрібно дільник помножити на частку.)
Учні легко можуть помітити, що вийшло відоме їм рівняння, і тому далі розв'язування вони коментують самі. х= 16-8 дг=128
— Виконаємо перевірку: 128 : (32 -24) = 128 : 8 = 16
16 = 16
— Перевірка свідчить, що корінь рівняння знайдений правильно. Розв'язування решти рівнянь виконується на дошці і в зошитах.
ФЬкультхвилинка
V. РОЗВИТОК МАТЕМАТИЧНИХ ЗНАНЬ
1. Колективна робота над задачею (с. 749, завдання 987)
— Що означає число 16?
— Що означає число 36?
— Що означає число 2?
— Що потрібно дізнатися в задачі? (Яку відстань проїхало авто?)
— Ми можемо відразу відповісти на це питання?
— Чому? (Спочатку ми повинні дізнатися скільки витратили бензину.)
— Ми можемо це дізнатися? (Так)
— Якою дією?
— Запишіть розв'язання задачі двома способами. Розв'язання
1й спосіб
1) 36 + 16-52 (л) — усього бензину;
2) 52 : 2 = 26 (раз.) — по 2 л у 52 л;
)10 • 26 = 260 (км)
2-й спосіб
1)16 : 2 8 (раз.) — по 2 л у 16 л;
2) 36 : 2 = 18 (раз.) — по 2 л у 36 л;
3) 10 • 8 = 80 (км) — на 16 л;
4)10•18 = 180 (км) — на 36 л;
5) 180 + 80 = 260 (км)
Відповідь: 260 км проїхало авто.
2. Робота над задачею з буквеними даними (с 150, завдання 988)
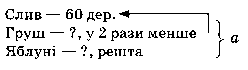
Розв'язання
1) 60 : 2 = 30 (дер.) — груш;
2) 60 + ЗО = 90 (дер,) — слив і груш;
3) а - 90 (дер.) — яблунь.
Відповідь: а — 90 розквітло яблунь.
3. Офтальмологічна пауза
4. Розв'язання логічних завдань
1) Завдання 989 (с. 150).
2) У потязі 11 вагонів. Наш вагон восьмий, якщо вести рахунок від голови потяга. Яким с цей вагон, якщо рахувати від хвоста потяга? Розв'язання: 11 — 8 = 3 — число вагонів, які знаходяться позаду 8-го вагона. Шуканий номер буде на 1 більшим. Маємо: (11 — 8)+ 1 = 4 — четвертий номер.
1; 2; 3; 4; 5; 6; 7; (8); 9; 10; 11. (4);(3);(2);(1).
VI. ПІДСУМОК УРОКУ
— Яку тему вивчали?
— Що нового ви дізналися на уроці?
VII. ДОМАШНЄ ЗАВДАННЯ С 150, завдання 990; 991.
|











